动态规划

山洞里有 \(M\) 株不同的草药，采每一株都需要一些时间 \(t_i\)，每一株也有它自身的价值 \(v_i\)。给你一段时间 \(T\)，在这段时间里，你可以采到一些草药。让采到的草药的总价值最大。

\(1 \leq T \leq 10^3, 1 \leq t_i, v_i, M \leq 100\)

• 朴素的 DFS 做法：
  

  cost = [0] * (100 + 5) # 采摘草药的时间
  get = [0] * (100 + 5) # 草药的价值
  
  res, T, M = 0, 0, 0
  
  # 准备选第几个物品、剩余的时间、已经获得的价值
  def dfs(pos, tleft, value):
      global res, T, M
      if tleft < 0:
          return
      if pos == M:
          res = max(res, value)
          return
      dfs(pos + 1, tleft, value)
      dfs(pos + 1, tleft - cost[pos], value + get[pos])
  
  
  def main():
      global res, T, M
      T, M = map(lambda x:int(x), input().split())
  
      for i in range(M):
          cost[i], get[i] = map(lambda x:int(x), input().split())
  
      dfs(0, T, 0)
      print(res)
  
  main()
  

  每株草药都有选与不选两种状态，时间复杂度是指数级别。同一个状态（pos, tleft）会被多次访问，所以效率较低。
  

  为了增加效率，可以在查询完一个状态后，将该状态存储下来，避免重复计算。
  

  
  

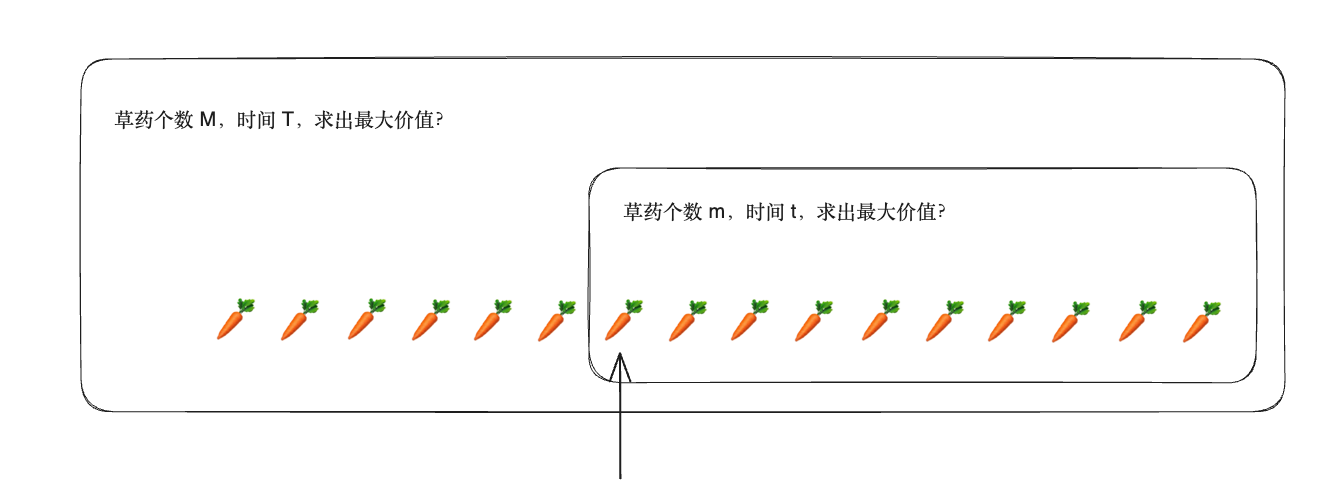
• 使用记忆化搜索优化
  

  增加 mem 数组记录每个 dfs(pos, tleft) 的返回值。 mem 中的初始值设为 -1 ，访问时如果是 -1 就继续递归访问，否则直接返回 mem 中存储的值。
  

  import sys
  
  cost = [0] * (100 + 5) # 采摘草药的时间
  get = [0] * (100 + 5) # 草药的价值
  mem = [[-1 for i in range(1005)] for j in range(105)] # 记忆数组
  
  inf = 0x3f3f3f3f
  
  res, T, M = 0, 0, 0
  # T 总时间
  # M 草药总数
  
  def dfs(pos, tleft) -> int:
      if pos == M:
          return 0
  
      if mem[pos][tleft] != -1:
          return mem[pos][tleft]
  
      dfs1 = dfs2 = -inf
      dfs1 = dfs(pos+1, tleft)
  
      if tleft >= cost[pos]:
          dfs2 = dfs(pos+1, tleft-cost[pos]) + get[pos]
  
      mem[pos][tleft] = max(dfs1, dfs2)
  
      return mem[pos][tleft]
  
  
  def main():
      # sys.stdin = open('input.txt', 'r')
      # sys.stdout = open('output.txt', 'w')
      global res, T, M
  
      T, M = map(lambda x:int(x), input().split())
  
      for i in range(M):
          cost[i], get[i] = map(lambda x:int(x), input().split())
  
      res = dfs(0, T)
      print(res)
  
  main()
  

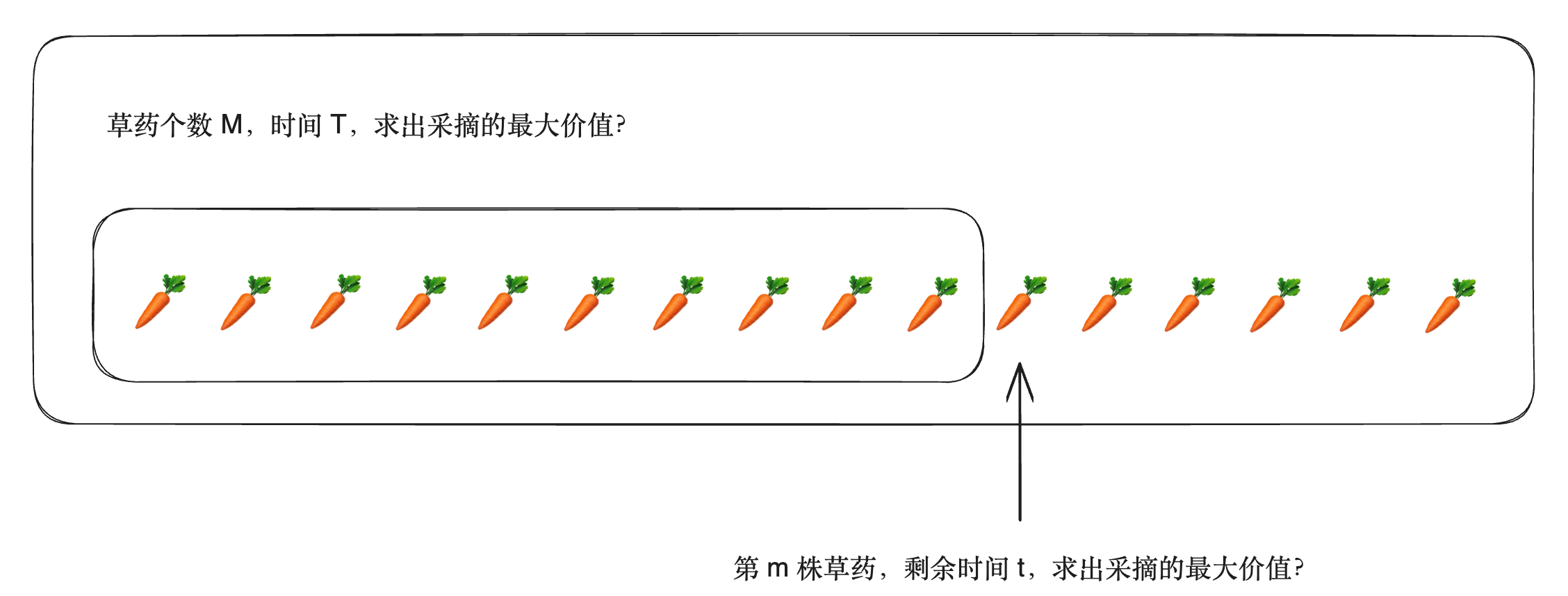
• 递推
  

  记忆化搜索和递推都可以用来求解动态规划问题。不同的是，递推通过明确的访问顺序来避免重复访问，记忆化搜索通过给已经访问过的状态打标记的方式避免重复访问。
  

  import sys
  
  cost = [0] * (100 + 5) # 采摘草药的时间
  get = [0] * (100 + 5) # 草药的价值
  
  res, T, M = 0, 0, 0
  # T 总时间
  # M 草药总数
  
  
  f = [[0 for i in range(1005)] for j in range(105)]
  def iteration() -> int:
      # t 时间
      # m 数量
      # -> v 价值
      for i in range(1, M+1): # 第几个
          for j in range(0, T+1): # 剩余时间
              f[i][j] = f[i-1][j] # 不选择当前草药
              if j >= cost[i]:
                  f[i][j] = max(f[i][j], f[i-1][j-cost[i]] + get[i])
  
      return f[M][T]
  
  
  def main():
      # sys.stdin = open('input.txt', 'r')
      # sys.stdout = open('output.txt', 'w')
      global res, T, M
  
      T, M = map(lambda x:int(x), input().split())
  
      for i in range(1, M+1):
          cost[i], get[i] = map(lambda x:int(x), input().split())
  
      res = iteration()
      print(res)
  
  main()
  

  
  

例题：

• 洛谷 P1434 滑雪